Options Price Calculator

Use the Options Price Calculator to calculate the theoretical fair value Put and Call prices, Implied Volatility, and the Greeks for any futures contract.

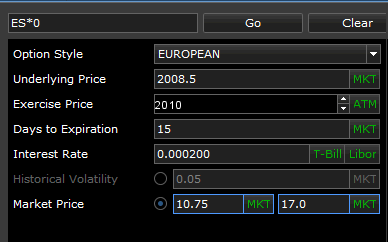
The calculator allows you to enter your own values (left side of screen). You can easily import the current market values for the variables by clicking the (MKT) button. Import the current T-Bill or Libor interest rates.

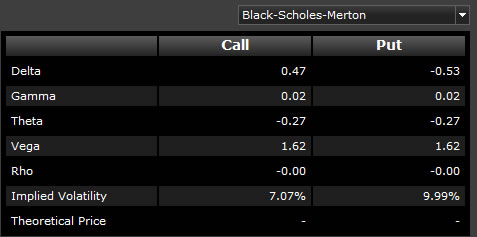
As you change the variables, the Put and Call prices along with the Greeks are recalculated and displayed on the right side of the screen:

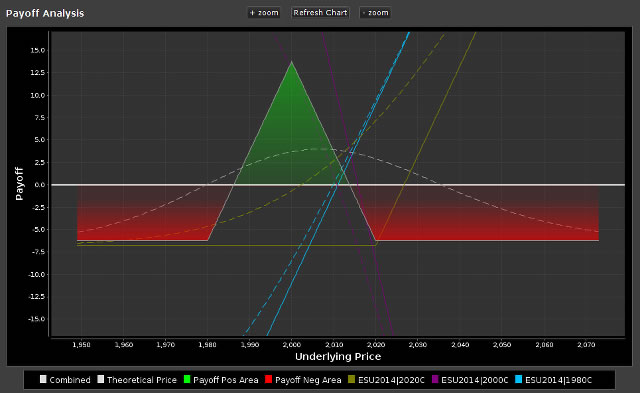
Potential payoffs are visualized on the Payoff Analysis Chart, with a Theoretical Price and Payoff table shown below.

Calculator Settings

Field / Column	Description
Pricing Method	Choose from either the Black-Scholes-Merton or Cox-Ross-Rubinstein (Binomial) method. The Black-Scholes-Merton method is generally used to calculate the theoretic values of the price of European options, where the Cox-Ross-Rubinstein method is used for American options.
Option Style	Choose from American or European options style. The major difference lies in when the options contract can be exercised. European options can only be exercised at the expiration date, where American options may be exercised at any time prior to the expiration date.
Underlying Price	The price of the underlying instrument. Click MKT to insert the current market price.
Exercise Price	The estimated exercise price of the underlying instrument. Click ATM to insert the current at-the-money price.
Days to Expiration	The number of days left till option expiration. Click MKT to insert the current days till expire of the closest option.
Interest Rate	The risk-free interest rate to use in calculations. Click T-Bill or Libor automatically insert the current rate for either.
Historical Volatility	Historical Volatility is a measure of how much the price of the underlying contract has changed over a certain period of time. It can be used to predict how likely future prices may change in the future. To calculate Theoretical Prices using Historical Volatility, click the radio button next to Historical Volatility. Next, click the MKT button to insert the current 20-day Historical Volatility for the underlying contract, or manually enter a number. Theoretical prices are then calculated for the Put and Call (shown on the right side of the screen) and the Greeks are recalculated.
Market Price	You can use the Market Prices of the Put and Call (for the Exercise Price shown above) to calculate Implied Volatility. Implied Volatility is the expected level at which the market thinks prices will go for the underlying contract. To calculate Implied Volatility using the Put and Call Market Prices, click the radio button next to Market Prices. Click the MKT button to insert the current Put or Call price, or manually enter a number. Implied Volatility is then calculated for the Put and Call (shown on the right side of the screen) and the Greeks are adjusted.

The Greeks

Field / Column	Description
Delta	Delta measures the sensitivity of an option's theoretical value to a change in the price of the underlying instrument. It is normally represented as a number between minus one and one, and it indicates how much the value of an option should change when the price of the underlying instrument rises by one dollar.
Gamma	Gamma measures the rate of change in the delta for each one-point increase in the underlying instrument. It is a valuable tool in helping you forecast changes in the delta of an option or an overall position. Gamma will be larger for the at-the-money options, and gets progressively lower for both the in- and out-of-the-money options. Unlike delta, gamma is always positive for both calls and puts.
Theta	Theta is a measure of the time decay of an option, the dollar amount that an option will lose each day due to the passage of time. For at-the-money options, theta increases as an option approaches the expiration date. For in- and out-of-the-money options, theta decreases as an option approaches expiration.
Vega	Vega measures the sensitivity of the price of an option to changes in volatility. A change in volatility will affect both calls and puts the same way. An increase in volatility will increase the prices of all the options on an asset, and a decrease in volatility causes all the options to decrease in value.
Rho	Rho is the sensitivity of option value to change in interest rate. Rho indicates the absolute change in option value for a 1% change in the interest rate. For example, a Rho of .060 indicates the option's theoretical value increases by .060 if the interest rate decreases by 1.0. Results may not be exact due to rounding. (source: Options Industry Council)
Implied Volatility	Implied Volatility can help traders determine if options are fairly valued, undervalued, or overvalued. It can therefore help traders make decisions about option pricing, and whether it is a good time to buy or sell options. Implied volatility is determined mathematically by using current option prices in a formula that also includes Standard Volatility (which is based on historical data). The resulting number helps traders determine whether the premium of an option is "fair" or not. It is also a measure of investors' predictions about future volatility of the underlying instrument.
Theoretical Price	The hypothetical value of the option, based on the calculations of the pricing model used.